Statistical Symbols and Definitions

 

Nielson, Jakob (1997). The use and misuse of focus groups. Retrieved August 28, 2006     from http://www.useit.com/papers/focusgroups.html.   Power Analysis (2003).  Retrieved August 28, 2006 from         http://www.statsoft.com/textbook/stpowan.html.   Michelle Jones, University of Phoenix, August 28, 2006

Symbols Provided by Tracie Williams-Algood, (UOPhx QNT 531, Fall 2004)

Baye's Theorem - as Baye originally intended. (Submitted by Lisa Cox UOP)  http://www.selfknowledge.org/resources/press/nyt_eakin.htm

Blocking - A portion of the experimental material that should be more homogeneous than the entire set of material (days, shifts, some other group). - Used to increase the precision of an experiment. Rational subgroup selected so that if assignable causes are present, the chance for differences between subgroups will be maximized, while the chance for differences due to these assignable causes within a subgroup will be minimized.

Box Plots -- Used to view the mean differences and distributions of spread or variability of the data. - To determine if they appear equal.

Cause and Effect Diagram - How to Construct:
(1) Define the problem or effect to be analyzed;
(2) Form the team;
(3) Draw the effect box and center line;
(4) Specify the major potential cause categories and join them as boxes connected to center line;
(5) Identify the possible causes and classify them into the categories in step 4 and create new categories, if necessary;
(6) Rank order the cause to identify those that seem most likely to impact the problem;
(7) Take corrective action.

Central Limit Theorem - Regardless of the distribution of the population the sum of n independently distributed random variables is approximately normal. The approximation improves as n increases.

Measures of Central Tendency describe and locate the center of the data:

1. Mean (average of data set) 

2. Sample mean (Xbar) 

3. Population Mean (m) 

4. Median (Sample median = x^~ = middle value) 

5. Mode (measurement that occurs most often)

Common Cause Variability - Controlled Variation

Continuous vs Discrete Data

Control Charts- Shows graphically, the results of many sequential hypothesis tests. UCL = m + Ls, Center Line =m,
LCL = m - Ls, Benefits: Improve Productivity, Defect Prevention, Prevent Unnecessary Process Adjustments, Diagnostic, Provide Process Capability Information. Mathematically equivalent to a series of statistical hypothesis test. Average Run Length (ARL) = 1/p = average number of points that must be plotted before a point indicates an out-of-control condition. P= probability that any point exceeds the CL. Average time to signal (ATS) = ARL (# Hour Sample Taken) = Time elapses (on average) between shift and its detection. "X = Average" and Variability "R = Range" Charts.

The Process is out of control if:

1. One point is out of 3-sigma control limits;
   

2. Two out of three consecutive points plot beyond the 2-sigma warning limits;
   

3. Four out of five consecutive points plot are a distance of 1-sigma or beyond from the center line;
   

4. Eight consecutive points plot on one side of the center line;
   

5. Six points in a row steadily increasing or decreasing;
   

6. Fifteen points in a row in zone C (both above and below the center line);
   

7. Fourteen points in a row alternating up and down;
   

8. Eight points in a row both sides of the center line with none in zone C;
   

9. An unusual or nonrandom pattern in the data;
   

10. One or more points near a warning or control limit.

Collectively Exhaustive Events - Events are collectively exhaustive if at least one of the events must occur when an experiment is conducted.

Controlled Variation (common cause variability) - many inherent sources of variation that affect the process in a random manner. The distribution of process output does not change overtime; thus, the pattern of variation is consistent and stable. Result from a large number of chance causes. Distribution of process output is stable over time. Removable only by process redesign. Examples: Machine vibration, environmental fluctuations, and human variation in setting equipment.

Conway, William B., Ex-president of Nashua Corp. Founded Conway Quality, Inc. in 1983. Quality Management. Eliminate waste of material and time. Right way to management rather than simply how to improve. New system of management whose primary task is continuous improvement which means changing all the unwritten rules in a company. Advocate of statistical methods to achieve quality gains. 85% of all problems can be solved by simple tools only about 15% require more complicate statistical process control methods. -

6 Tools for Quality Improvement
(1) Human relation skills
(2) Statistical surveys
(3) Simple statistical techniques
(4) Statistical Process Control
(5) Imagineering
(6) Industrial Engineering

Crosby, Philip B. - Book Quality is Free, Defines quality as conformance to requirements and can only be measured by cost of non-conformance. Prevention (means perfection) is the word summing quality. No place for statistical levels of quality. Three ingredients - (1) determination, education, and implementation. Management's responsibility (should be as concerned about quality as profit).

Zero Defects as a management performance standard.
(1) make it clear that management is committed to quality.
(2) Form quality improvement teams with representatives form each department.
(3) Determine where current and potential quality problems lie.
(4) evaluate the cost of quality and explain its use as a management tool.
(5) Raise the quality awareness and personal concern of all employees.
(6) Take actions to correct problems identified through previous steps.
(7) Establish a committee for the zero defects program.
(8) Train supervisors to activity carry out their part of the quality improvement program.
(9) Hold a zero defects day to let all employees realize that there has been change.
(10) Encourage individuals to establish improvement goals for themselves and their groups.
(11) Encourage employees to communicate to management the obstacles they face in attaining their improvement goals.
(12) Recognize and appreciate those who participate.
(13) Establish quality councils to communicate on a regular basis.
(14) Do it all over again to emphasize improvement never ends.

Data, Types of - Variable (anything measurable) and attribute (counting data, good or bad, conforming or nonconforming).

Distribution, Probability - Mathematical model that relates the value of the variable with the probability of occurrence of the value in the population. Continuous Distribution - Variable being measured is expressed on a continuous scale. Discrete Distribution - Parameter being measured can only take on certain value, such as integers 0,1,2,….

Degrees of Freedom - Are the number of independent elements that go into a statistic.

Demings, Dr. W. Edwards - Believes responsibility for quality rests with management, and the power of statistical methods. "People who expect quick results are doomed to disappointment." Good quality is nor necessarily high quality. It is predictable degree of uniformity and dependability, at low cost and suited to the market. Statistical control doses not imply absence of defective items. It is a state of random variation, in which the limits or variation are predictable. Two type of variation: Chance and Assignable. Not enough to meet specifications; one has to keep working to reduce the variation. Advocate of worker participation in decision making. Management action is required to improve quality (94% of all issues). Inspection is designed to allow a certain number of defects to enter the systems. (Vendors should be under statistical control. Advocates single sourcing.

(1) Create a constancy of purpose focused on the improvement of products and services.
(2) Adopt a new philosophy of rejecting poor quality.
(3) Do not rely on mass inspection to control quality.
(4) Do not award business to suppliers of the basis of price alone but also consider quality.
(5) Focus on continuous improvement.
(6) Practice modern training methods and invest in training for all employees.
(7) Practice modern supervision methods.
(8) Drive out fear.
(9) Break down the barriers between functional areas of the business.
(10) Eliminate targets, slogans, and numerical goals for the workforce.
(11) Eliminate numerical quotas and work standards.
(12) Remove the barriers that discourage employees from doing their jobs.
(13) Institute an ongoing program of training and education for all employees.
(14) Create a structure in top management that will vigorously advocate the first 13 points.

Erlang - Developed queuing for handling telephone switchboard problems.

Error -- ÎI,j = Yi,j - Average Yj.

Event - An event is the collection of one or more outcomes of an experiment.

Exhaustive Data - Each individual, object, or measurement must appear in one of the categories.

Experiment - A test in which purposeful changes are made to input - So that we can observe and Identify Changes in Outputs of a Process.  An experiment is the observation of some activity or the act of taking some measurement. 

Experimental Error Variance - MSE = E(s^2)

Feigenbaum, Dr. Armand V. - First introduced the concept of company -wide quality control in his book Total Quality Control. More concerned with organizational structure and a systems approach to improving quality than he is with statistical methods, important, as quality improvement does not usually spring forth as a "grass roots" activity; it required a lot of management commitment to make it work. Once suggested that the technical capability be concentrated in a specialized department, this differs form the more modern view that knowledge and use of statistical tools need to be widespread.

Fixed Effects Model - E(MSTRT) = s^2 + (n(åtI^2))/(a-1) Where (I=1,2…a)

Fuzzy Logic - http://plato.stanford.edu/entries/logic-fuzzy  (submitted by Cyndi Cox UOP).

Grand Mean - Overall Mean

Graphical method -- from section 3-5.3 - SDV = s/(n)^1/2 @ (MSE/n)^1/2 - Draw Normal Curve with Grand average and lower and upper limits, then place other data averages on curve.

Histogram - (1) Count number of observation in the sample (2) Determine the range of values in the sample (3) Determine the class interval size (4) Establish class midpoints and boundaries (5) Determine class boundaries (6) Tally numbers of observations to fall in each class (7) Construct histogram

Class With = Range /(number of classes you want)

Class Relative Frequency = (Class Frequency) / (Total Number of Measurements (n))

Hypothesis (from Larry Buess of Trevecca) -- A hypothesis is a measurable statement about a condition you suspect exists today that supports an objective.  The hypothesis is a guess about the strength of a current condition and is usually stated as a proportion (a percent) or in some cases as a significant strength.  The hypothesis does not depend on any intervention or future events.  You know or suspect a problem or need exists today, but you have to measure how big the problem or need is..

Examples:
  
Objective:  Within 3 months after implementing the new tube filler procedure, there will be a 30% increase in production at the Oxydent toothpaste factory in Nolensville, TN.
 
The “what” of this objective is “increase in production” .   The new tube filler procedure is the intervention.  The hypothesis must support “increase in production” and not reasons for the new tube filler procedure.
 
Possible hypotheses could arise from questions such as::
 
   Why does production need to increase?
 
Hypothesis 1.1  Production at the Nolensville plant is 10% below the average of other Oxydent factories in the USA.
 
Hypothesis 1.2  Production at the Nolensville plant is 15% below production of all toothpaste factories in Tennessee.
 
Hypothesis 1.3  Production at the Nolensville plant has decreased by over 26% during the last 2 years.
 
     How do employees feel about production?
 
Hypothesis 1.4  Over 75% of the employees feel that production could be higher.
 
Hypothesis 1.5  Over 80% of the supervisors feel that production must increase.
 
      Another possible hypothesis:
 
Hypothesis 1.6  Over 30% of our Oxydent toothpaste distributors have orders that can’t be filled.

Independent Events - Events are independent if the occurrence of one event does not affect the occurrence of another.

Juran, Dr. Joseph M. -- One of the founding fathers of Statistical Quality Control. Co-authored the Quality Control Handbook. Less focused than Dr. Deming on statistical methods. Philosophy based on organization for change and the implementation of improvement through "managerial breakthrough" which is a structured problem-solving process. Management action is required to improve quality (80% of all issues). Species of Quality: - Structural, Sensory time orientated, commercial, and ethical. Two kinds of quality: fitness for use and conformance to specifications. Three basic steps: structured annual improvements combined with devotion and sense of urgency. All major problems are interdepartmental. Quality is not free. Likes quality circles. Law of diminishing returns where changes become too costly. Not in favor of single sourcing. Training for purchasing managers should include rating vendors. No such thing as improvement in general. Improvement is going to come about project by project and no other way.

10-steps to Quality Improvement
(1) Build awareness of the need and opportunity for improvement.
(2) Set goals
(3) Organize to reach the goals,
(4) Provide training
(5) Carry out projects to solve Problems
(6) Report progress
(7) give recognition,
(8) Communicate results,
(9) Keep score,
(10) Maintain momentum by making annual improvement part of the regular systems and processes of the company.

Levels of Measurement:

1. Nominal level of data is classified into categories and cannot be arranged in any particular order.

2. Ordinal level involves data arranged in some order.  However, the differences between data values cannot be determined or are meaningless. (Such as the which athlete is first second.)

3. Interval level is similar to the ordinal level However, meaningful amounts of differences between data values can be determined. There is no natural zero point. (example in book is temperature.)

4. Ratio level has an inherent zero starting point. Differences and ratios are meaningful for this level of measurement.

Mean = sum of all observations divided by the number of observations.

1. Discrete Mean and Average

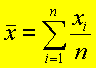
Question: What would be the effect on the mean if all observations are multiplied by the same constant? 

Answer: The mean is also multiplied by the constant. Same goes with division.

Mutually exclusive - An individual, object, or measurement is included in only one category.  Events are mutually exclusive if the occurrence of any one event means that none of the others can occur at the same time.

Nonparametric - Definition quoted from ...W. J. Conover, Practical Nonparametric Statistics 2nd ed, 1980, John Wiley and Sons, Inc, page 92.

" A statistical method is nonparametric if is satisfies at least one of the following criteria:

1. The method may be used on data with a nominal scale of measurement.

2. The method may be used on data with an ordinal scale or measurement.

3. The method may be used on data with an interval or ratio scale of measurement, where the distribution function on the random variable producing he data is either unspecified or specified except for the infinite number of unknown parameters."

Normal Probability Plots - Is a plot of data (either raw data or residuals) against percent cumulative normal probability. - To check assumptions of normality. If normal the data will follow a linear line with data parts near the line, which is sometimes tested by covering these points with a pencil.

Normally Distributed Populations 

Outcome - An outcome is the particular result of an experiment. 

Outliners - If there is reason to suspect that the point was not a legitimate collection, then it can be ignored. Otherwise, it points to a need for investigation.

Parameter - is a measurable characteristic of a population.

Probability - It is a measure of the likelihood of an event occurring. We can obtain probabilities by experience, subjective ways or counting

Quality - Fitness for use which will include the fit, form and function. Fitness of use is based on customer requirements. Quality is inversely proportional to variability.

Quality Characteristics - (1) Physical (Length, weight, voltage, viscosity); (2) Sensory (Taste, appearance, color); (3) Time Orientation (Reliability, durability, serviceability).

Quality Cost -- Reasons to consider 1. Increase in the complexity of manufactured products associated with advances in technology. (2) Increasing awareness of life cycle cost (maintenance, labor, spare parts, and cost of field failures). (3) Need for quality professionals to effectively communicate the cost of quality. Prevention Cost - Quality planning and engineering, New products review, product & process design, Process control, Burn-in, Training, Quality data acquisition and analysis. Appraisal Costs - Inspection and test of incoming, material , product inspection and test, materials and services consumed, maintaining accuracy of test equipment. Internal Failure Cost - Scrap, Rework, Retest, Failure Analysis, Downtime, Yield Losses, Downgrading (off-specing). External Failure Costs - complaint adjustment, Returned product/material, Warranty charges, liability, Indirect costs.

Quality, Dimensions of - 1. Performance (will the product do the intended job?); 2. Reliability (how often does the product fail?); (3) Durability (how long does the product last?); (4) Serviceability (how easy is it to repair the product?; (5) Aesthetics (what does the product look like?); (6) Features (what does the product do?); (7) Perceived Quality (what is the reputation of the company or its product?); (8) Conformance to Standards (is the product made exactly as the designer intended?); (8+1) Use (is the product used as envisioned?)

Quality Engineering the set of operational, managerial, and engineering activities that a company uses to ensure that the quality characteristics of a product are at the nominal or required levels.

Quality Improvement is the reduction of variability in processes and products.

Quality Program Evaluation - (1) Quality of materials, (2) accuracy and precision of measurement systems, (3) Knowledge, ability, techniques and support (time) to control the process over a long period of time (4) Capability of a process measured over a short period of time (5) Modifying system for ht process to ensure that the control techniques are operating properly (6) Company policies concerning continuous Improvement

Queuing - Developed by Erlang for handling telephone switchboard problems. Used arrival rates, service rates, number of servers type information to find information related to server use, average waiting times, probability of waiting times exceeding a certain limit, average length of queue, Average waiting times in queue and in system.

Randomization - Both the allocations of the experimental material and the order in which the individual runs or trials of the experiment are to be performed are random - To Eliminate Biases.

Random Effects Experiments - Have the following in common: (a) treatments are random sample from a larger population, (b) tI I=1,2,3,…a are random variables, (c) Test of hypothesis is about the variability of tI

Random Effects Model -- E(MSTRT) = s^2 + (n * sT^2)

Random Error Component - See Experimental Error Variance

Rational Subgroup - Subgroups or samples selected so that the assignable causes are present, the chance for differences between subgroups will be maximized, while the chance for differences due to these assignable causes within a subgroup will be minimized. (see blocking).

Regression Significance Test -- bo = ma; b1 = m1 -ma;; b2 = m2 - ma ;…….

Residuals - See step five above.

Replication - Duplication of the same test where all controls are the same - Used to get an estimate of error and to estimate the central tendency related to mean and variability to observe differences in the data to determine if they are really statistically different. If the sample mean is used this permits the experimenter to obtain a more precise estimate of effects.

Shewhart, Walter -- Father of SPC - While every process displays variation, some processes display controlled variation (common cause variability), while others display uncontrolled variation. Defined Special-Case Variability and Common Cause Variability.

Statistics - What is Statistics? – A Study of how to best (a) Collect Data, (b) Describe and Summarize Data, and (c) Draw Practical Conclusions Based on Data. A way to: test theories and practices in some cases related to doing work determine the characteristics of a population by using a sample Using data to make inferences under uncertainty Big Picture - Science of amassing data, taking a portion of it, and seeing what that portion tells us about the whole Little Picture - actual statistics themselves statistics with little “s” is any number that represents something else.

Statistical Process Control -- Program Elements - (1) Management Leadership, (2) A team approach. (3) Education of Employees at all levels. (4) Emphasis on Continuous Improvement. (5) A mechanism for recognizing success and communication this throughout the organization. Goal to remove all special-cause variation, so that process is predictable. Characteristic parameters like the mean, standard deviation, and probability distribution are constant. Can determine -Process Capability, if redesign is economically feasible, affect on the final product. Benefits - Increase Customer Satisfaction, Decrease scrap, rework, inspection, operation cost, Maximize productivity, Establish a predictable and consistent level of quality.

Special-Case Variability -- see Uncontrolled Variability

Special Rule of Addition - If two events A and B are mutually exclusive, the special rule of addition states that the probability of A or B occurring equals the sum of their respective probabilities: P(A or B) = P(A) + P(B)

Subjective Approach - Based on opinions could have different approaches.

Total Variability - SST

Transformations - Used to analyze data that is non-normal in its standard form (but becomes normal in the transformed form) or data that has unequal variance.

Treatment Effects - See 4.3 above

Type I Error -- a = r (reject Ho|Ho is true)

Type II Error -- b = r (fail to reject Ho|Ho is false) ---Power = 1-b = r (reject Ho|Ho is false)

Types of Data: 

1. Qualitative or Attribute variable is nonnumeric.

2. Quantitative variable information is numeric.

   1. Discrete variables can only assume certain values (such as counting the number of cars).

   2. Continuous variables can assume any value within a specified range (such as height of a person).

   

   From an example in book.

Uncontrolled Variability - Special-Case Variability - typically results from the influence of one or two identifiable sources. Sources also known as assignable cause variability tend to be unpredictable and may come and go. Distribution of process output is unstable and unpredictable. Removable by systematic identification and elimination on the shop floor. Examples: Operator error, inferior raw stock, over adjustment, and poor setup.

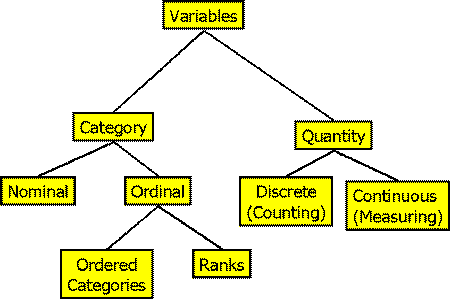
Variable Types

1. Category (Less Exact)

   1. Nominal Variable (Name)

   2. Ordinal Variable (relative condition) 

      1. Ordered Categories 

      2. Ranks 

2. Quantity

   1. Discrete Variable (countable units, integers)

   2. Continuous Variable (infinite but measurable possible events)

Variability Between Treatments - E(s^2) = (MSTRT - MSE)/n
Variability, Types of - Controlled Variation (Common Cause Variability) and Uncontrolled Variation (Special-Cause Variability)